March 2025: Hall of Mirrors 3
March 2025: Hall of Mirrors 3
Date: March 2025
Link: click here
Solved on: March 12, 2025
The Puzzle
We are given an empty 10x10 grid of squares with lasers pointing into the grid on every edge. Some lasers have numbers assigned to them. We are tasked with placing mirrors such that each laser enters and exits the maze, and that the product of the laser’s lengths within the maze equal its assigned number on the outside.
Initial Observations/Questions
- By looking at the sample puzzle, the laser beam is split into its assigned number’s prime factors (well, most of the time).
- Remember that mirrors cannot be placed orthoganny adjacent, so you cannot chain together laser lengths of 1.
Strategy
Note: The following strategy may not be the most efficient process to solve the problem, but it is how I went about it in my head.
As every mirror was placed, I wanted to make sure that there were no other options to reduce the amount of times I had to backtrack. I started with the upper right corner $1$. Since mirrors cannot be placed next to each other (in orthogonal directions), the only option was to put a mirror in the topmost right corner. This also forces the nearby $4$ to simply move 2 units, hit the mirror, then move 2 units to the edge. The other option here, 4 units then 1 unit, is impossible since it would have no other way of reaching the edge.
As mirrors were being placed, marking (I highlighted cells in yellow, for instance) each cell with a laser going through it, a mirror, or orthogonally adjacent to a mirror, narrowed down possible options. It is honestly a bit hard to describe my thought process at this point in hindsight, but with the process of elimination and making sure each mirror I placed did not have any other options, I was able to get the final board. With that, you can add up the side values to get the final answer.
Answer
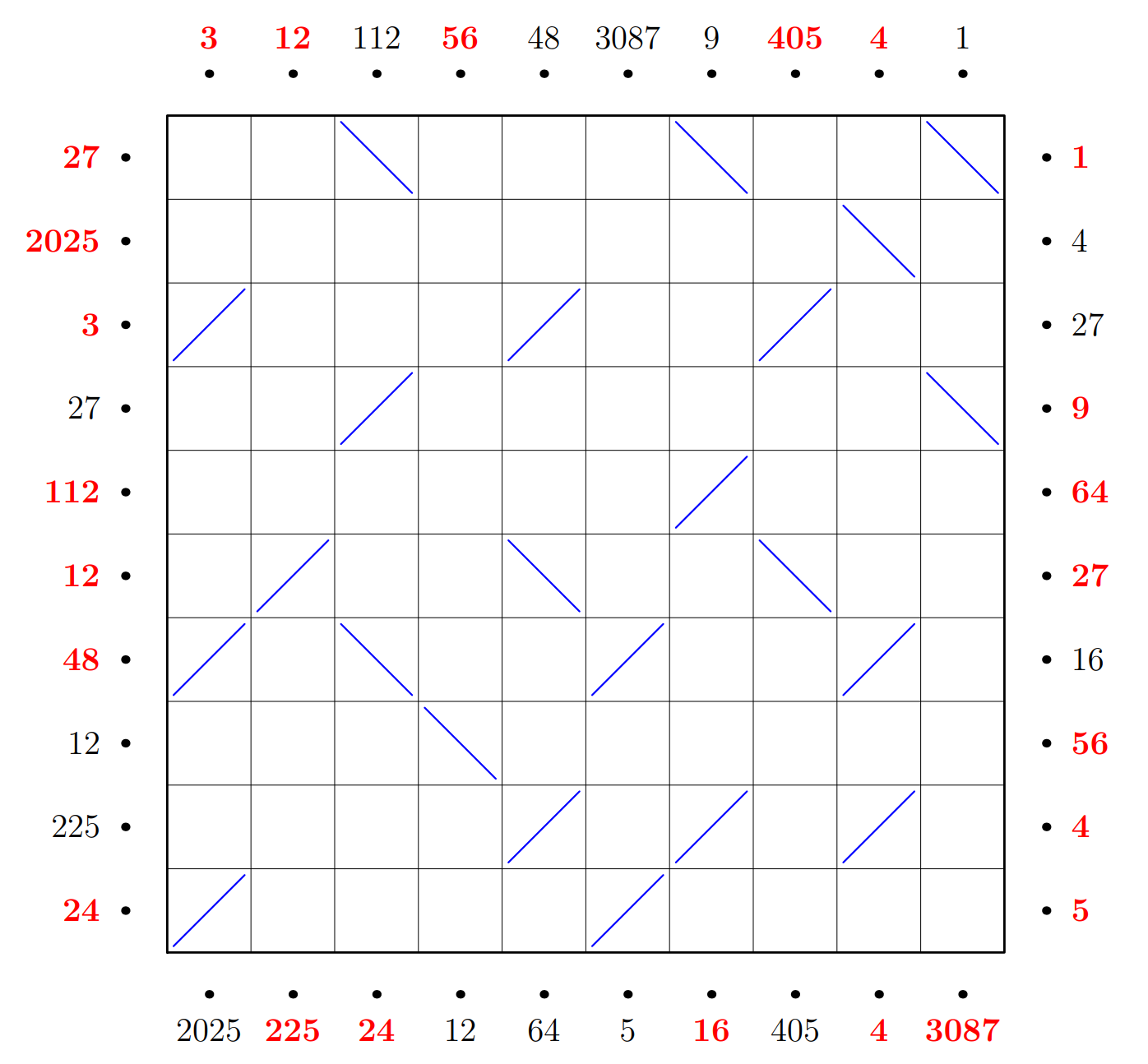
The missing clue numbers are in red in the image above. Clockwise from the top they sum to $480$, $166$, $3356$, and $2251$. This gives a product of $601,931,086,080$.
About Me
I am currently a Sophomore at Northeastern University studying Computer Science and Mathematics, with a goal to work in the quantitative finance field. I love working through these type of problems and using code to make the solution more elegant. More information on me and some projects I’m proud of can be found on my website below.