April 2025: Sum One, Somewhere
April 2025: Sum One, Somewhere
Date: April 2025
Link: click here
Solved on: April 11, 2025
The Puzzle
The puzzle description is pretty short, so here it is in full:
For a fixed $p$, independently label the nodes of an infinite complete binary tree $0$ with probability $p$, and $1$ otherwise. For what $p$ is there exactly a $\frac{1}{2}$ probability that there exists an infinite path down the tree that sums to at most $1$ (that is, all nodes visited, with the possible exception of one, will be labeled $0$). Find this value of $p$ accurate to 10 decimal places.
Initial Observations/Questions
- This is a straight math/programming question, and I didn’t think that the puzzle name or description held any clues/hints for this type of puzzle.
Strategy
Note: The following strategy may not be the most efficient process to solve the problem, but it is how I went about it in my head.
The first thing I did was think “what is the probability, in respect to p, that there exists a path down the tree that sums to at most 1.” For this, there are two cases.
Case A: Path is All Zeros
Let the probability that the path is all zeroes be denoted by $P_0(p)$, where $p$ is stated in the prompt.
This can be further split into three sub-cases:
-
Path of zeroes exists only on the left side
-
Path of zeroes exists only on the right side
-
Path of zeroes exists on both sides
We calculate the probabilities as follows:
- Only on the left side:
- Only on the right side:
- On both sides:
Now, the total probability that the path is all zeroes (in any of the above forms) is the sum of the three:
\[P_0^{\text{total}}(p) = P_{\text{left}} + P_{\text{right}} + P_{\text{both}} = 2 \cdot P_0(p) \cdot (1 - P_0(p)) + P_0(p)^2\]Now, we simplify the total probability expression:
\[P_0^{\text{total}}(p) = 2P_0(p)(1 - P_0(p)) + P_0(p)^2\]Expanding:
\[= 2P_0(p) - 2P_0(p)^2 + P_0(p)^2 = 2P_0(p) - P_0(p)^2\]Letting $P_0(p) = P$ for simplicity, we get:
\[P_0^{\text{total}}(p) = 2P - P^2\]Now, recall the recursive formulation: a path of all 0s exists if the root is 0 (probability $p$ and at least one child subtree contains a path of all 0s. The probability that neither subtree contains such a path is $(1 - P)^2$), so the probability that at least one does is $1 - (1 - P)^2$. Therefore:
\[P = p \cdot (1 - (1 - P)^2) = p \cdot (2P - P^2)\]Bringing all terms to one side:
\[P - p(2P - P^2) = 0\]Expanding:
\[P - 2pP + pP^2 = 0\]Rewriting:
\[P(pP + (1 - 2p)) = 0\]So either:
\[P = 0 \quad \text{or} \quad pP + (1 - 2p) = 0\]Solving the second equation:
\[pP = 2p - 1 \\ P = \frac{2p - 1}{p}\]Therefore, the total probability $P_0$ is either:
\[P_0 = 0 \quad \text{or} \quad P_0 = \frac{2p - 1}{p} = 2 - \frac{1}{p}\]Now, back to the other case.
Case B: Path Exists with at Most 1 One:
The goal here is to define $P_1(p)$, and so along with $P_0(p)$ above, we’ll be able to solve for $p$.
Thus, let $P_1(p)$ be the probability that a given node’s subtree contains some path that uses at most one node labeled 1. To start, let’s look at the root node.
| root label | probability | requirement on (at least one) child subtree |
|---|---|---|
| 1 | (1-p) | the path has already spent its single 1, so the child subtree must supply an all‑zero path ⇒ probability $P_0$ |
| 0 | (p) | the path may still contain ≤ 1 One in the descendants ⇒ probability $P_1$ |
So, we can combine both cases into a simple equation, where the first term is if the root is $0$ and the second if the root term is $1$:
\[P_1 \;=\; p\,\bigl(2P_1-P_1^{2}\bigr)\;+\;(1-p)\,\bigl(2P_0-P_0^{2}\bigr).\]Move all terms to one side:
\[0 = -pP_1^2 + P_1(2p-1) + (1-p)P_0(2-P_0)\]Since we know $P_0 = 2 - \tfrac1p$ for $p>\tfrac12$, we have:
\[2P_0 - P_0^2 = \frac{2p - 1}{p^2}\]so,
\[-p\,P_1^2 + (2p - 1)\,P_1 + (1-p)\,\frac{2p-1}{p^2} = 0\]Now that all $P_0$ are substituted for, we can set $P_1 = \tfrac12$ (the puzzle’s “exactly 1/2” condition):
\[-\,p\Bigl(\tfrac14\Bigr) \;+\; (2p-1)\Bigl(\tfrac12\Bigr) \;+\; \frac{(1-p)(2p-1)}{p^2} = 0.\]Remove denominator by multiplying through by $4p^2$:
\[-p^3 + 2p^2(2p-1) + 4(1-p)(2p-1) = 0 \;\Longrightarrow\; 3p^3 - 10p^2 + 12p - 4 = 0.\]Therefore the cubic equation is \(\boxed{3p^3 - 10p^2 + 12p - 4 = 0}\)
whose unique root in $(\tfrac12,1)$ is
\[p \approx 0.5306035754.\]Checking the Answer
I wanted to check my answer to make sure that I hadn’t made any mistakes in the math process.
First, I made a recursive function that simulates a single traversal down a complete binary tree, with each node’s value generated on the fly according to the given $p$. It returns True if there exists a path down the tree with at most $k$ ones.
def simulate_valid_path(depth, k, p):
if depth == 0:
return True
val = 0 if random.random() < p else 1
if val == 1:
k -= 1
if k < 0:
return False
return simulate_valid_path(depth - 1, k, p) or simulate_valid_path(depth - 1, k, p)
Then, you can estimate the probability that a given path exists by running many independent simulations with a given $p$. The following function returns the fraction of runs where a valid path down the tree (at most $k$ ones) was found.
def estimate_probability(p, depth, k, trials):
success = 0
for _ in range(trials):
if simulate_valid_path(depth, k, p):
success += 1
return success / trials
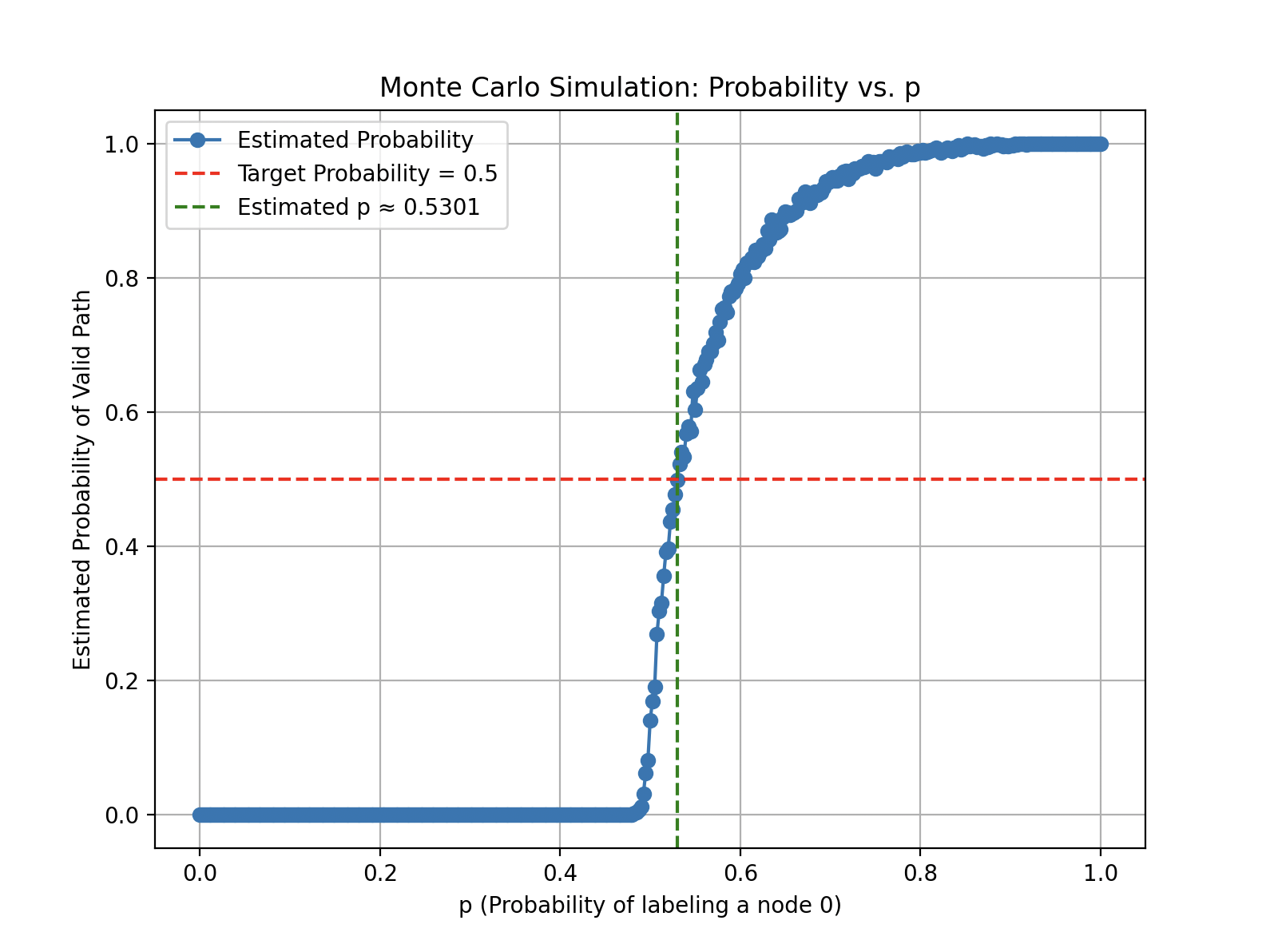
Then, we can run a monte-carlo simulation with the above functions:
# Simulation parameters
depth = 250 # depth of binary tree simulation
k = 1 # the problem allows for up to 1 one
trials = 1000 # trials to test
p_values = np.arange(0.0, 1.0001, 0.0025) # values of p to test
estimated_probs = []
# Running simulation for different p values...
for p in p_values:
prob = estimate_probability(p, depth, k, trials)
estimated_probs.append(prob)
estimated_p = np.interp(0.5, estimated_probs, p_values)
plt.figure(figsize=(8, 6))
plt.plot(p_values, estimated_probs, marker='o', linestyle='-', label="Estimated Probability")
plt.axhline(0.5, color='red', linestyle='--', label="Target Probability = 0.5")
plt.axvline(estimated_p, color='green', linestyle='--', label=f"Estimated p ≈ {estimated_p:.4f}")
plt.xlabel("p (Probability of labeling a node 0)")
plt.ylabel("Estimated Probability of Valid Path")
plt.title("Monte Carlo Simulation: Probability vs. p")
plt.grid(True)
plt.legend()
plt.show()
Running the code shows the visualization, predicting a very close number to what was calculated before.
Answer
Thus, I was confident the answer was $0.5306035754$.
About Me
I am currently a Sophomore at Northeastern University studying Computer Science and Mathematics, with a goal to work in the quantitative finance field. I love working through these type of problems and using code to make the solution more elegant. More information on me and some projects I’m proud of can be found on my website below.